◇ 作家：中国银行上海总部金融阛阓部主宰　王文滨开云·Kaiyun体育(中国)官方网站 登录入口

　　森浦二级往来惩办决议业务主宰　王乃身

　　森浦二级往来惩办决议居品众人　吴小伟

　　中国银行上海总部金融阛阓部业务司理　袁骏青

　　◇ 本文原载《债券》2024年11月刊

　　摘   要

　　本文尝试从往来角度构建实时利率弧线，弘扬基于该弧线的订价决议，弘扬数据中式和清洗决议，在给定债券投资组合的情况下弘扬基于实时利率弧线的关节期限基点价值对冲策略，并检会该弧线的对冲成果。与其他考虑不同，本文把流动性较好的国债期货居品融入利率弧线构建和对冲之中，具有较强的实施带领真谛。

　　关节词

　　Nelson-Siegel模子　利率弧线　弧线订价　对冲模子

　　东说念主民币债券阛阓照旧成为公共第二大债券阛阓，但国内债券阛阓的流动性结构和报价价差依然存在提高空间。当今阛阓上对通盘固定收益钞票的订价往往基于光滑零息利率弧线对不同期限的现款流贴现。而作念市商需要实时利率弧线用于作念市和为阛阓提供流动性；投资机构需要实时利率弧线实时发现往来契机，并可用于风险计量和对冲往来。荒谬是关于对冲往来，更需要基于其本身能得到的报价和可用的对冲用具构建日内可成交利率弧线。

　　跟着金融科技与电子化往来的发展，实时利率弧线众多性更为突显，故探讨构建实时利率弧线具有极大的经济价值。本文尝试从更实务的往来和对冲角度提供一个实时利率弧线构建的能力论。

　　本文主要分为四个部分：一是弘扬实时利率弧线构建的能力论，包括弧线模子、无套利分析；二是弘扬基于该弧线的订价决议；三是弘扬数据中式和清洗决议；四是分析该弧线订价端正，并在给定债券投资组合的情况下弘扬基于实时利率弧线的关节期限基点价值对冲策略。

　　实时利率弧线构建的能力论

　　（一）弧线模子分析

　　利率弧线中的静态模子，主要通过拟合不雅测数据构造，包括非参数法和参数法。本文主要筹商参数法，包括Nelson-Siegel（NS）模子偏激拓展表情Svensson（SV）模子等，因其参数浅易方便考虑，且具有宏不雅真谛。

　　NS模子中，即期利率的抒发式为：

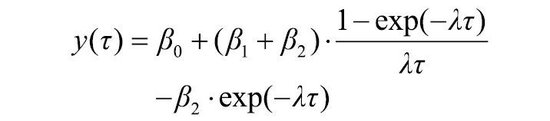
　　式中，τ=T-t，默示估值日历t至到期日T的剩余期限，βi（i=1，2，3）为模子参数。由模子推导可知：

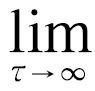
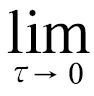
　　y（τ）=β0+β1。β0为水平因子，代表永远利率水平；β1代表斜率因子，β2为曲率因子。

　　y（τ）=β0，

　　为提高利率弧线的拟合生动性和精度，Svensson（1994）提议了NS模子的膨胀模子，即在NS 模子上添加两个新参数，允许弧线出现第二个“驼峰”去拟合弧线在远端期限的曲率特征，由此组成SV 模子。

　　Diebold and Li（2006）进一步在NS模子的基础上提议了动态NS（DNS）模子。模子假设将原NS模子中的三个固定参数（β0，β1，β2）变为成三个一阶自追忆经过。

　　（二）无套利分析

　　上述三个模子都莫得从表面上确认模子为无套利。Duffie和Kan（1996）提议仿射利率模子，假设利率与因子间存在线性仿射表情，并基于风险中性测度对债券进行订价，因此具有无套利特征。其中，零息债券价钱为景况变量的仿射函数：

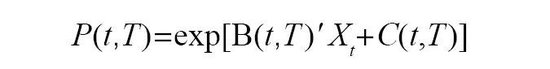
　　Christensen、Diebold和 Rudebusch（2011）在仿射利率模子基础上提议了无套利NS（Arbitrage-Free Nelson-Siegel，AFNS）模子。要使得仿射利率模子具有NS模子的特征，要求仿射利率模子中零息债券价钱中因子整个方程B（t，T）的解知足NS模子参数方程抒发式，即

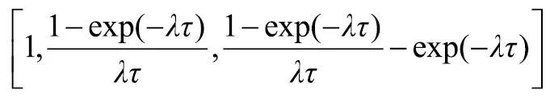
　　Coroneo、Nyholm和Vidova-Koleva（2011）实证考虑了NS模子具有无套利特征。考虑继承了重抽样本事，基于NS模子生成样本，将该样本用于无套利仿射利率模子，检会端正是仿射利率模子得到的因子整个方程B（t，T）与NS模子的因子整个方程B（t，T）在统计上无死别，确认NS模子具有无套利特征。

　　本文华纳NS模子，情理是：领先，该模子便于快速实时考虑，方便本体欺诈；其次，该模子参数具有一定的经济学含义；终末，如上所述，该模子表面上不错诊疗为无套利仿射模子，统计上也合计该模子为无套利，其订价妥贴阛阓平衡特征，其中隐含的经济信息更具有代表性。

　　实时利率弧线订价决议

　　（一）参数计算

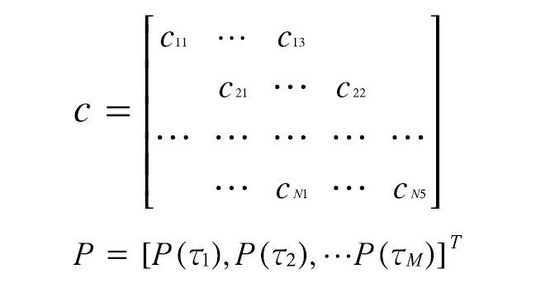
　　本文弧线参数由基准券计算得出，假设N只基准债券的价钱向量为PV=[pv1， pv2，…， pvN]T，证据每只债券的基本信息可考虑现款流，假设cij为第i只债券的第j笔现款流。假设N只债券合计有M笔现款流，求解弧线即求解下列方程：PV=cP，其中c为现款流矩阵，P为零息债券价钱，即贴现函数。其具有如下表情：

　　上式中，贴现函数P（τ）=exp[-y（τ）∙τ]，τj=Tj-t，t为估值日，Tj为第j笔现款流到期支付日。P（τ）可由即期利率弧线模子推算出，利率弧线函数为τi→y（τi）。弧线参数计算需要使得基于弧线的现款流贴现模子价钱与现券阛阓价钱之间尽量接近，即求解以下优化问题：

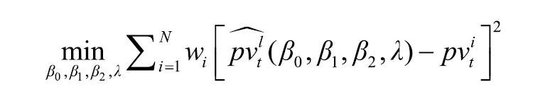
　　上式中，pvti为债券i阛阓价钱，

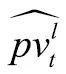
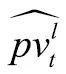
　　jcijP（τj），wi为债券i权重。往往债券权重选择为债券久期的倒数。

　　（二）实时利率弧线订价

　　Jankowitsch和Nettekoven（2008）考虑发现常用的弧线模子并不成皆备准确地对债券订价，存在订价舛讹（pricing error）。订价舛讹往往由于债券的税收和流动性不同，但大部分这方面考虑无法确认一起舛讹项。剩余订价舛讹部分是由模子设定罪过或特定时段债券价钱偏离市模式致。该作家提议了一个基于债券订价舛讹的往来策略，能得到显耀的禀报。作家还发现债券订价舛讹具有一定的趋势抓续性，并不皆备是立地的。

　　基于以上琢磨，本文实时弧线订价及舛讹考虑处理逻辑如下：

　　一是基于前几期弧线考虑债券对应期估值与行情价钱之差动作模子订价舛讹；行情价钱优先选择收盘成交价，要是不存在则选择交易（bid/ofr）中间价。

　　二是考虑前几期订价舛讹的滚动均值。

　　三是构建面前最新弧线，证据最新弧线考虑债券理讲价钱，将弧线理讲价钱加上舛讹滚动均值，动作最终模子估值。

　　四是获取最新有用阛阓行情，更新订价舛讹。

　　（三）实时利率弧线评价

　　弧线模子选择的直不雅考量尺度是订价准确性和对冲成果，同期需要兼顾弧线考虑的方便性、表面 上的一致性等。同期，也需要琢磨弧线的理解性，即弧线受单个数据点的波动影响较小，当数据小幅变动时弧线变动不应更大。

　　数据中式与清洗决议

　　国债期货与利率互换动作常用的对冲用具，相似包含与阛阓利率关系的信息。为使弧线更能反应面前阛阓景况，本文加入国债期货参与构建弧线。本文中式国债期货主力合约参与弧线构建：在主力合约可交割券中选择往来最活跃券，将国债期货价钱乘以诊疗因子动作该券在期货结算日的债券全价。

　　为使得弧线包含更多有用信息，数据的处理相似众多。

　　（一）荒谬数据处理

　　由于手动输入罪过或其他操作造作等，行情存在荒谬报价。该类报价明显大幅偏离面前阛阓行情。是以数据处理先需过滤荒谬数据。

　　本文的荒谬数据过滤章程为：当成交价钱偏离最近3分钟阛阓行情最优价均值迥殊20BP，则绮丽为荒谬数据，将其过滤。

　　（二）倒挂数据处理

　　不同渠说念佛纪商报价不成告成撮合成交，当行情存在倒挂时，手动报价撮覆没不成立即排斥倒挂契机。本文在假设倒挂行情存在成交可能性下，在两者之间概括选择，保留部分信息。其处理章程如下：与上一笔行情相比，取保守价钱。

　　（三）基准券权重

　　由于权重不同，弧线受不同券行情波动的影响不同，进而影响弧线对不同券的订价。因此本文在权重中琢磨了每只券的往来活跃度。本文在逐日日初固定基准券权重，取上一往来日成交笔数的对数ln（X）+2，X为成交笔数。

　　实时利率弧线订价端正

　　本文基准券选择章程如下：关于固息国债和策略性金融债，选择昔时一周成交量活跃且上一往来日存在往来的债券，其中剔除剩余期限不及1年及上市已迥殊3年的债券，剔除含权债、浮息债、贴现债。另外加多国债期货主力合约。最终的实时利率弧线端正如图1所示。

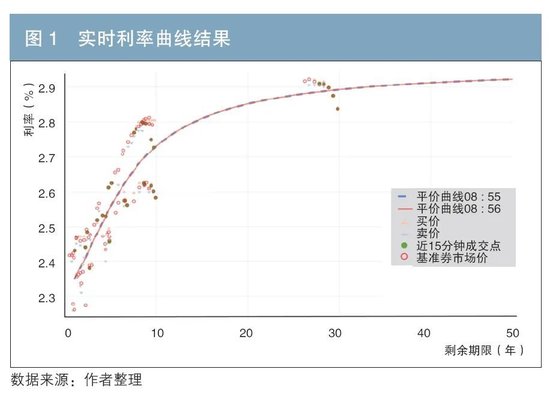
　　图1为2023年12月22日08∶56基于行情构建的平价弧线（Par Curve），其由零息弧线考虑得出。其中虚线为上一分钟弧线，实线为面前这一分钟弧线。其中红色空腹圆圈为参与构建弧线基准券的阛阓行情，绿色实心圆点为成交行情，凹凸三角形分别代表交易报价。

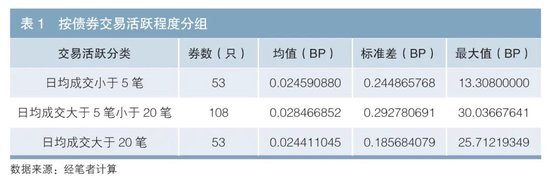
　　为检会本文能力对债券的订价端正，本文华纳2023年12月19日的一组债券数据。该组债券合计215只，其中包含政府债券82只、策略性金融债133只，含活跃券和非活跃券。数据时间段为08：30至18∶30，按分钟频率统计最终订价与成交行情的舛讹。其中以前5个往来日日均成交笔数动作债券活跃度主义，将债券分散为3组：小于5笔、大于5笔小于20笔、大于20笔。其订价端正如表1所示。端正领略越活跃债券的订价舛讹均值和尺度差越小，这与预期一致。其中“最大值”一列领略某券订价舛讹的最大值。由于订价券中存在剩余期限小于0.1年的债券，其行情及订价波动较大，但全样本债券订价波动尺度差为0.23BP支配。

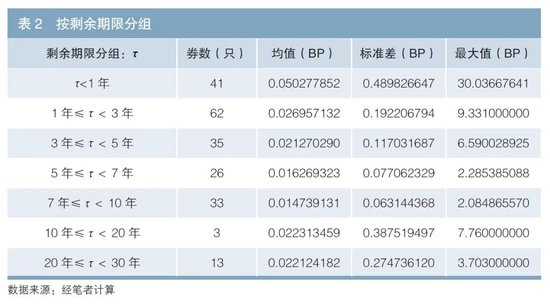
　　对不同剩余期限债券的订价端正如表2所示。表2领略，在10年期限以内，当期限加多，弧线订价端正均值和舛讹减小，订价更精确；而大于10年的债券订价与期限间莫得明显关系，可能与关整个据样本量偏小关系。剩余期限大于10年的债券相对小于1年的短期债券，短期债券波动更大，荒谬偏离也更大。短期限债券更容易受弧线变动影响，这与NS模子的特色相符。

　　基于往来弧线关节期限基点的价值对冲策略

　　（一）对冲模子

　　本文华纳债券投资组合中基准组合构建代表性投资组合，检会弧线对冲成果。假设抓仓组合值为V0，存在i个风险度量主义，存在L个可用的对冲用具，其值为H=（H1， H2， ．．．， HL）T，对冲用具对因子的明锐性为∂iHl，假设对冲用具的权重为p=（p1， p2， ．．．， pL）T，对冲组合的价值为H（p）=pT·H。该组合对因子的明锐性为∂iH（p）=pT∙∂iH。那么对冲的主义是尽可能对冲掉抓仓组合V0对该因子的明锐性风险∂iV0。对冲组合问题诊疗为一个优化问题。该优化问题的主义函数为：

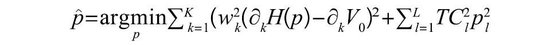
　　上式中，假设TCl为该对冲用具的往来老本。若界说矩阵∂H=[∂1H， ∂kH， ．．．， ∂kH]，∂V0=[∂1V0， ．．．， ∂kV0 ]T，假设权重矩阵W的对角上元素为Wk，往来老本矩阵TC对角上元素为TCl，那么上述问题滚动为：

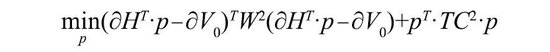
　　上述问题的解为：

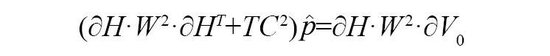
　　（二）往来老本

　　在债券阛阓中存在交易非同步性和信息不合称，使得往来存在老本。其中交易的非同步性导致作念市商或投资者需要被迫抓有一段时间，并濒临价钱波动带来的损益。信息不合称是往来老本存在的另一个众多原因：不同债券刊行者、不同债券条件对投资者传递的信息含量不同。在进行对冲时需要琢磨往来老本。本文中，往来老本TC=Dt×BA，Dt为订价期初债券久期，BA为交易价差。

　　（三）风险明锐性考虑

　　本文中钞票组合的利率明锐性主义为关节期限基点价值（KRDV01，以下简称“关节期限DV01”），为弧线在关节期限上变动1个基点对债券价钱的影响，可证据关节期限久期（KRD， Key-Rate Duration）考虑。国债期货的风险明锐性由前文所述可交割券考虑，即可交割券的明锐性除以诊疗因子。

　　（四）对冲策略

　　本文对冲策略是在关节期限DV01上设定两个风险阈值。当组合关节期限DV01达到第一个阈值1时，且抓仓组合风险较小时，证据债券往来流动性，选择阛阓行情最优价挂单卖出已抓有债券。在此情形下，需要琢磨挂单至被点击成交的时间老本，当成交时，作念市商的抓仓量减少，同期作念市商不错得到交易价差。当组合关节期限DV01达到第二个阈值2时，此时在国债期货等活跃钞票上对冲，不错对冲该关节期限DV01，同期减少其他关节期限DV01风险。

　　为检会往来弧线偏激对冲成果，本文华纳抓仓组合如下：由短期枪弹策略、中期枪弹策略、永远枪弹策略构建的梯形组合。组合中包含债券如下：1年期债券（包含140029.IB、220332.IB）、3年债券（包含220002.IB、210315.IB）、5年期债券（包含180027.IB、190205.IB）、10年期债券（包含130016.IB、230205.IB）、30年期债券（包含230009.IB、210221.IB）。组合总抓仓面值1亿元，每个组合内每只券抓仓面值1000万元。

　　组合继承对冲用具为30年期国债期货（TL2403）、2年期国债期货（TS2403）、10年期国债期货（T2403）、5年期国债期货（TF2403）。在2023年12月28日考虑对冲端正如表3所示。表中关节期限为0.5年、1年、2年、3年、5年、7年、10年、15年、30年。抓仓组合中单券的关节期限DV01如表3所示，从该券场所行第4列驱动，对应的期限列中领略该券在该期限的关节期限DV01。那么当组合合计风险敞口在设定关节期限中迥殊阈值1时（本例中以10年期限关节期限DV01值迥殊5000元）进行第一步对冲。以表3中230205.IB为例，其价差在2023年12月28日最低时为0.25BP，10年期关节期限DV01为5289.66元，总基点价值（DV01）为8162.05元，那么挂卖单进行对冲可赢利2040元。

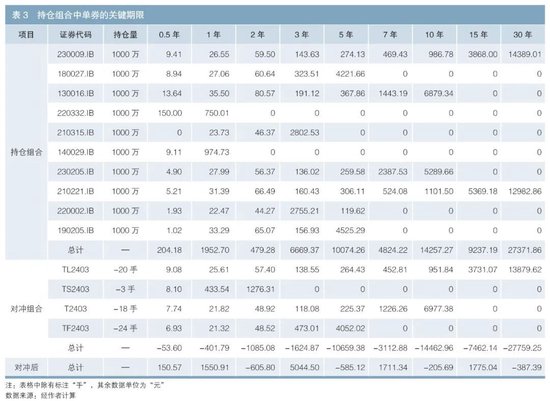
　　当在设定关节期限中迥殊阈值2时（本例中以5年、10年巧合30年的关节期限DV01阈值迥殊10000元时）进行国债期货对冲。本例通过在国债期货TL2403上空20手、TS2403上空3手、T2403上空18手、TF2403上空24手，对冲老本为4220元，不错对冲掉抓仓组合中在5年、10年、30年期上利率波动的大部分风险。

　　论断

　　本文从本体往来角度开赴，提议了基于往来和对冲的实时利率弧线构建能力论，其中会通了国债期货，使得弧线反应了更多的阛阓信息，况且对阛阓波动反应更飞速。数据分析端正领略，NS模子对活跃券的订价相比准确、理解，但其短端订价波动较大，与NS模子特征相符。这不错动作将来的纠正优化标的。另外，组合的对冲分析需要琢磨往来老本，不同对冲用具的往来老本不同。由于国债期货往来活跃，其往来老本相对较低，本文的分析案例选择国债期货动作对冲用具。

　　参考文件

　　[1]Christensen J H， Diebold F X， Rudebusch G D， The affine arbitrage-free class of Nelson–Siegel term structure models[J]． Journal of Econometrics， 2011，164 （1）．

　　[2]Coroneo L， Nyholm K， Vidova-Koleva R， How arbitrage-free is the Nelson-Siegel model？[J]．Journal of Empirical Finance[J]．2011，18（3）．

　　[3]Diebold F X， Li C， Forecasting the Term Structure of Government Bond Yields[J]．Journal of Econometrics， 2006，130（2）．

　　[4]Duffie D， Kan R， A Yield-factor Model of Interest Rates[J]． Mathematical Finance， 1996，6（4）．

　　[5]Jankowitsch R， Nettekoven M， Trading strategies based on term structure model residuals[J]． The European Journal of Finance， 2008，14（4）：281-298．

　　[6]Leif B G Andersen， Vladimir V Piterbarg． Interest Rate Modeling[M]． Illustrated edition． Atlantic Financial Press， 2011．

　　[7]Nelson C R， Siegel A F， Parsimonious Modeling of Yield Curves[J]． Journal of Business，1987，60（4）．

海量资讯、精确解读，尽在新浪财经APP

遭殃剪辑：赵念念远 开云·Kaiyun体育(中国)官方网站 登录入口